实验一：一维小波变换的实现

题目

给定小波母函数：

$\Psi = (\frac{2}{\sqrt{3}}\pi^{-\frac{1}{4}})(1=x^2)e^{-\frac{x^2}{2}}$

有效支撑为$[-5,5]$以及信号$f(t)$（从data.mat 文件读取，400 个数据，采样间隔为 0.03）。

做连续小波变换，结果以图像形式给出（尺度-位移）。

要求：确定连续小波的采样间隔，尺度范围大致在 1 到 70 之间，选取以能使大部分信号能量落在该范围为准。实验不得调用现成的 cwt 函数。

解题思路

构造母小波函数，以方便后续生成不同尺度下的离散小波。
通过两层for循环嵌套，计算不同尺度下、不同位移的小波与原始信号的互相关值，并生成二维系数矩阵。
计算原始信号和母小波的自相关值，从而得到归一化后的小波变换结果。
通过plot和pcolor函数生成最终图像，以直观展示结果。

理论基础

母小波的离散化处理及放缩位移变换

母小波：

$\Psi(x) = (\frac{2}{\sqrt{3}}\pi^{-\frac{1}{4}})(1=x^2)e^{-\frac{x^2}{2}}$

小波的缩放平移公式：

$\Psi_{a,b}(t) = \frac{1}{\sqrt{a}}\Psi(\frac{t-b}{a})$

尺度a下、对母小波进行采样（）：

$\Psi_{a}[k] = \frac{1}{\sqrt{a}}\Psi(\frac{k}{a}) \tag{k:[0:399]}$

为方便后续互相关计算，取采样后的序列长度与原信号保持一致。

对离散母小波进行平移有

$\Psi_{a,b}[k] = \frac{1}{\sqrt{a}}\Psi(\frac{k-b}{a}) \tag{k:[0:399]}$

小波变换中系数的计算

小波变换（母小波为实小波）

$W_f(a,b) = \int_{-\infty}^{+\infty}f(t)\Psi_{a.b}(t)dt$

对于取定的a,b，即计算小波与原信号的互相关值。

对于离散信号有：

$R_{12}[0]=\sum_{k=-\infty}^{+\infty}f[k]\Psi_{a,b}[k]$

在本题中，k的取值范围为[0:399]，即完整信号。前面提到，采样后的序列长度与原信号保持一致，目的为此处不需要做补0处理。

结果的归一化处理

此处计算的互相关值无实际意义，因此对结果做归一化处理，使零滞后时的自相关等于 1。

$R^{'}_{xy}[0] = \frac{1}{\sqrt{R_{xx}[0]R_{yy}[0]}}R_{xy}[0]$

其中$R{xx}$和$R{yy}$分别为原信号和母小波信号的自相关值。

需要说明的是，因为母小波的经过尺度和平移变换后，信号未必完整，信号能量发生变化，为使结果具有参考意义，使用尺度和平移变换前的完整的离散母小波进行计算。即：

$R_{xx}[0] = \sum_{k=-\infty}^{+\infty}f^{2}[k] \\ R_{yy}[0]=\sum_{k=-\infty}^{+\infty}\Psi^{2}_{a,b}[k]$

matlab实现

clc;clear;

% 定义常量
DT = 0.03;  % 采样间隔 
% 小波有效支撑范围
WAVELET_START = -5;  
WAVELET_END = 5;
% 尺度范围
a_MIN = 1;
a_MAX = 70;

load 'data.mat';
len = length(dat);
t=(0:len-1).*DT;
% plot(t,dat);

x = linspace(WAVELET_START, WAVELET_END, len);
wavelet = (2/3^(1/2)*pi^(-1/4))*(1-x.^2).*exp(-x.^2/2);
% plot(x,wavelet);


% 小波变换结果（ab系数矩阵）
result = zeros(a_MAX,len);
% 初始化离散化小波
wavelet_d = zeros(1,len);


for a = a_MIN:a_MAX

% 不同尺度下的离散小波
for k = 1:len
wavelet_d(k) = base_wave(k/a);
end

for b = 1:len
R12 = (sum(wavelet_d.*dat))/sqrt(a);
result(a,b) = R12;  % 未归一化
% 移位
wavelet_d=[base_wave(-1*b/a),wavelet_d(1:len-1)];
end
end

% 原始数据和小波的自相关系数: 归一化处理
R11 = sum(dat.*dat);
R22 = sum(wavelet.*wavelet);
result = result./sqrt(R11*R22);

% 绘图
figure(1);
% 原始数据
subplot(2,2,1);
plot(t,dat);
title('原始数据');
xlabel("时间 t/s");
% 小波母函数
subplot(2,2,2);
plot(x,wavelet);
title('小波母函数');
% 尺度与位移谱图
subplot(2,2,3);
pcolor(result);
title('尺度与位移谱图');
xlabel("位移 b");
ylabel("尺度 a");
% 尺度与位移三维谱图
subplot(2,2,4);
surf(result);
title('尺度与位移三维谱图');
xlabel("时间位移");
ylabel("尺度");

% 母小波函数
function out=base_wave(in)
if abs(in)<=5
out=(2/3^(1/2)*pi^(-1/4))*(1-in^2)*exp(-in^2/2);
else
out=0;
end
end

实验结果

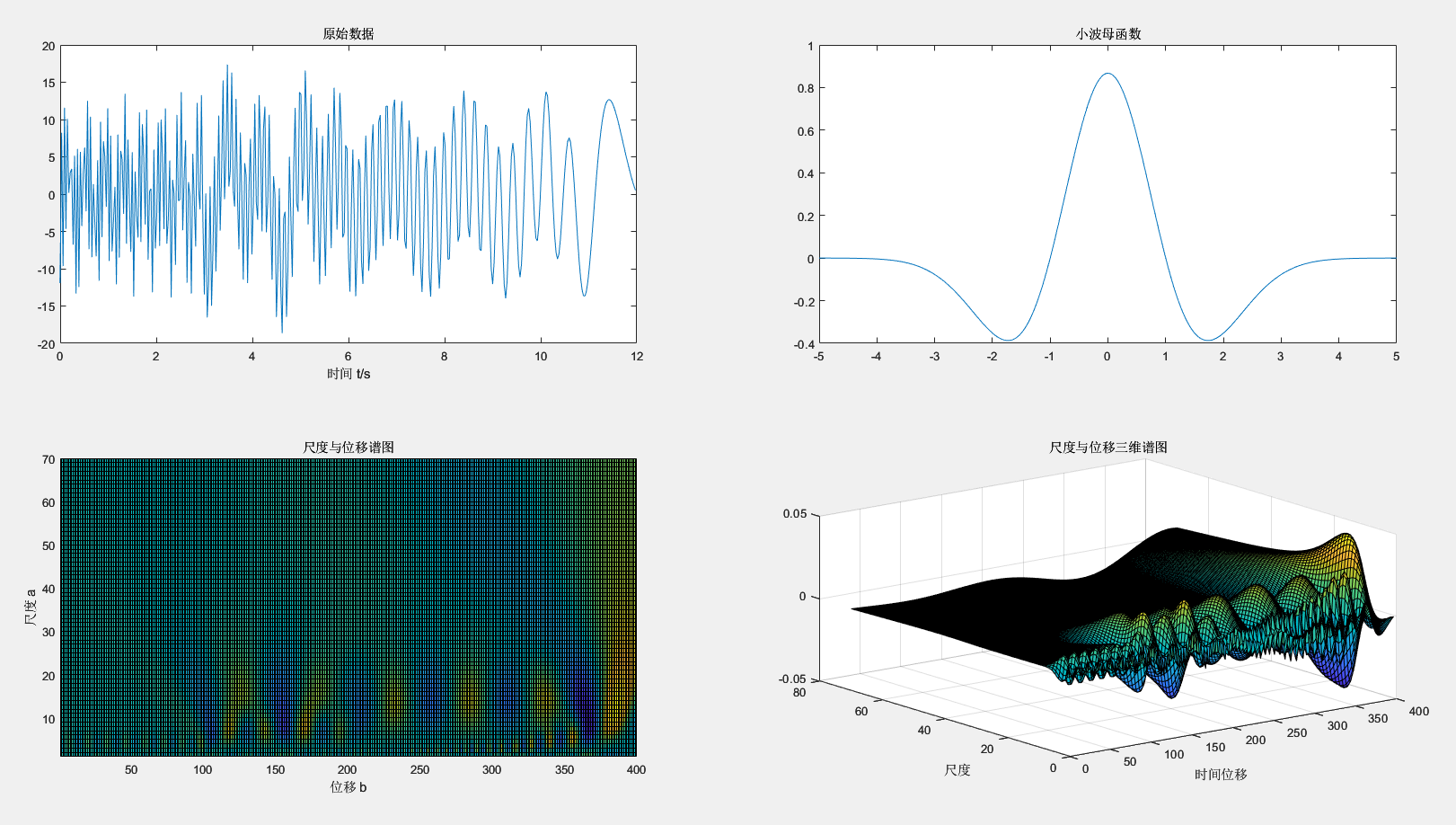
总览

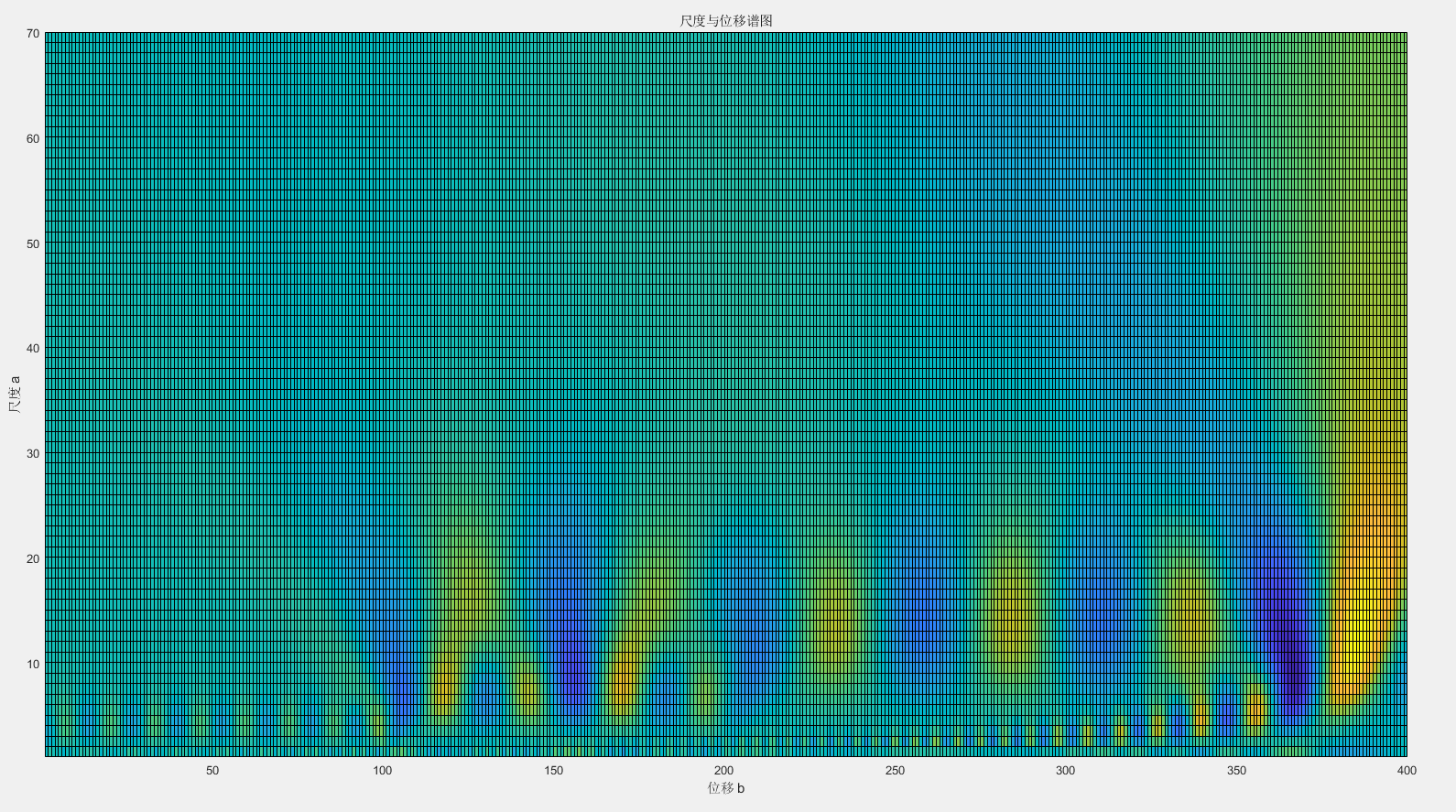
尺度与位移谱图

尺度与位移三维谱图

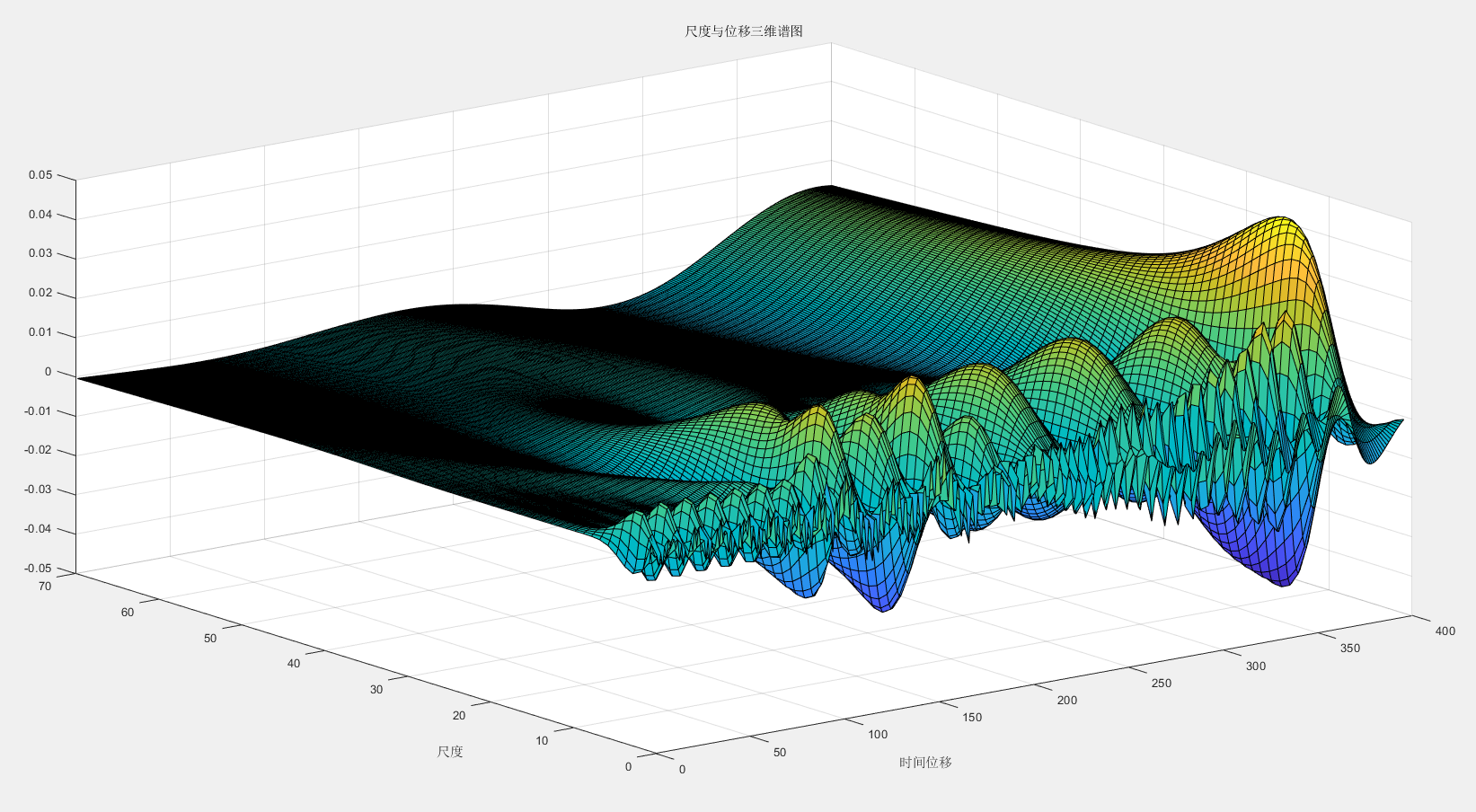
结果分析

参看实验原始数据图像，信号的频率与随时间变化存在明显变化。在前几秒频率较高，随后频率降低。

在尺度与位移谱图中，在时间的前段时间信号主要集中在高频部分（小尺度）；随后低频部分（大尺度）出现大的波峰和波谷并扩大。

实验结果与分析一致。